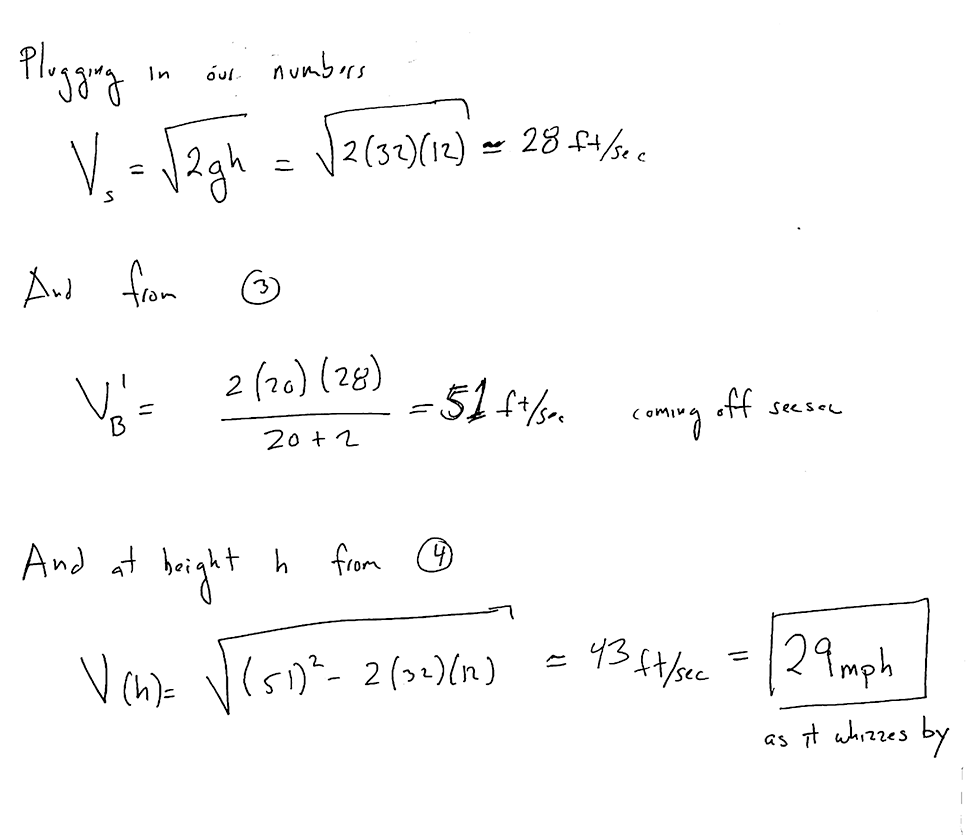A Brick and a Seesaw
Related Episode
Update: Solution below
Related Episodes
Pick up your pencils everyone! At the top of this week’s show Ira interviewed Graeme Patterson who, when he was a kid, did an experiment with a brick and a seesaw that did not go as planned. Graeme told us in the interview that he’d often wondered if you could calculate how fast the brick would have been going as it whizzed past his head. I wondered that too! I actually spent way too much time wondering about it, with a pen and paper. I did it wrong the first time. But (after checking with two Harvard physicists) I think we have the right answer.
It’s actually a pretty good intro physics problem. I’ve written it up as it might appear in a textbook. Send us your answers if you like. We’ll post the solution later this week.
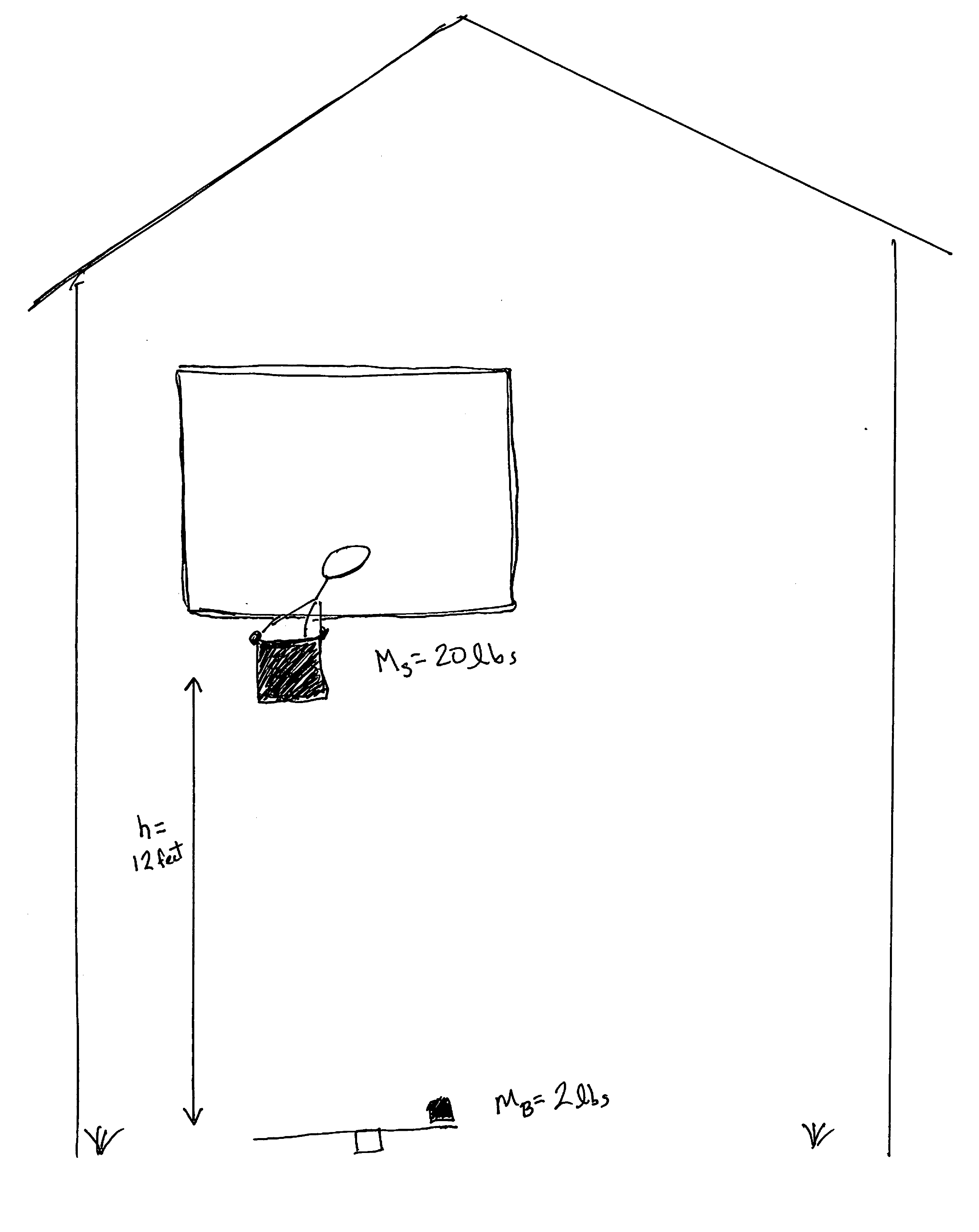
Graeme is playing at a construction site and wants to launch a brick high into the air. He makes a seesaw out of a plank of wood, balanced on a brick at the center. He puts a second brick (the one he wants to launch) on one end of the seesaw. Then he climbs up to the second floor of a half-finished house and drops a large block of concrete onto the other end of the seesaw. If the mass of the brick is 2 lbs, the mass of the block is 20 lbs and he drops the stone from a height of 12 feet, how fast is the brick moving when it whizzes by him at height h? (For simplicity assume the collision is elastic and that the teeter-totter is massless and starts out horizontal. Ignore air resistance.)
Solution
Pencils down! I see one of you took an experimental approach to answering the question. Very impressive! (Videos here and here.)
Since we are assuming the collision is elastic (no energy is lost from the brick, stone and seesaw system) both energy and momentum must be conserved. This gives two equations which, with a little algebra (see below), can be combined and solved to give the velocity of the brick coming off the seesaw. (In this case 51 feet/sec ⋍ 35 mph.) The brick then slows due to gravity as it rises.
By the time it whizzes by Graeme it would be moving at 29 mph.
It may be tempting to think that all the momentum of the stone is transferred to the brick - that the stone hits the seesaw and immediately comes to rest and the brick goes flying off. But that only happens if the mass of the stone and brick are equal. (Think about two billiard balls hitting head-on, in that case one does stop and the other takes up the momentum.) If the stone is heavier than the brick, then the brick takes some of the momentum but the stone does not stop. In fact because the fulcrum is in the center of the seesaw, the solution here is actually the same as for what happens if two blocks or balls collide on a (frictionless, one-dimensional) table. That one is in the textbooks.
Thanks to David Morin and Melissa Franklin at Harvard for checking this. David writes, by the way:
I thought of another argument why the resulting speed is the same as in the linear case of one ball simply colliding with another: Assuming a rigid seesaw, it actually doesn’t need to be straight. It could be bent by any angle in the middle, and the smaller ball will still come out at the same speed (but at a different, angle, of course); the conservation of E and L equations are the same. So you can imagine bending one radial arm all the way back around to the other, making the angle between them zero (instead of 180 for a straight seesaw). In this extreme case, the seesaw effectively consists of only one (doubled up) radial arm. So we basically have one ball hitting another ball, with an irrelevant board in between. Removing the irrelevant board then just gives a standard one-dimensional collision. (A picture is probably worth at least 100 words here.)
And then for a standard 1-D elastic collision in the limit where one ball is much more massive than the other, the easiest way (in case this reasoning has faded from your memory!) to get the resulting speed of 2v is to temporarily work in the reference frame of the large ball. The small ball comes in at speed v and then simply bounces out with (essentially) speed v (assuming an elastic collision). Switching back to the lab frame involves adding on the speed v of the large ball, yielding 2v total for the small ball.
The approximation that the velocity of the brick coming off the seesaw is twice the velocity of the stone when it hits isn’t bad in this case. You get a final velocity of about 33 mph which is pretty close.